Площу фігур будемо позначати «S». Площа вимірюється у одиницях довжини в квадраті, тобто: «м²», «см²» і так далі.

Площа трикутника

Для будь якого трикутника ми можемо використовувати будь які з наступних формул (1-5):

1. Якщо маємо сторону трикутника («a») та висоту проведену до цієї сторони («h_a») можна використати таку формулу:

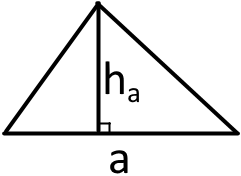
S = /1/2 ah_a

2. Якщо маємо дві сторони трикутника («a», «b») та кут між цими сторонами («y»):

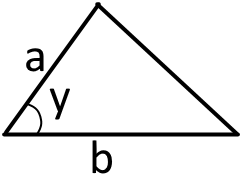
S = /1/2 ab sin ⁡y

3. Якщо відомі всі сторони трикутника («a», «b», «c»), то необхідно знайти півпериметр «p» (половина периметра трикутника).

p = /P/2 = /a + b + c/2

Варто зауважити, що півпериметр має вийти більшим за будь яку зі сторін трикутника. Після чого скористатися такою формулою (ця формула має особисту назву «формула Герона»):

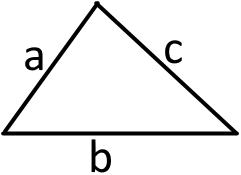
S = p(p - a)(p - b)(p - c)

4. Якщо у трикутник вписане коло (або ще кажуть, що трикутник описаний навколо кола) і відомо радіус («r») цього кола та відомі всі сторони трикутника («a», «b», «c») або відомий периметр «P», то необхідно знайти півпериметр «p».

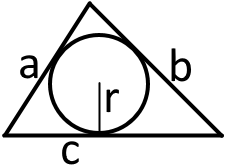
p = /P/2 = /a + b + c/2

Після чого площу шукаємо за такою формулою:

S = pr

5. Якщо навколо трикутника описане коло (або ще кажуть, що трикутник вписаний у коло) і відомо радіус («R») цього кола та відомі всі сторони трикутника («a», «b», «c»), то площу можемо знайти за такою формулою:

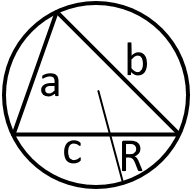
S = /abc/4R

Для прямокутного та рівностороннього трикутника можна використовувати формули (1-5) та їх особисті.

6. Якщо є прямокутний трикутник в якому відомі катети («a», «b»), то можна використати таку формулу:

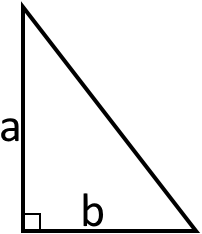
S = /1/2 ab

На справді це є формула під номером «2». Просто між катетами прямокутного трикутника знаходиться кут «90» градусів. А на «sin⁡ 90⁰ = 1». Тому його вже і не записують.

7. Якщо є рівносторонній трикутник в якому відома сторона («a»), то можна використати таку формулу:

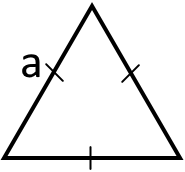
S = a² 34

Знову ж таки це є формула під номером «2». Але відразу перетворена для рівностороннього трикутника. Оскільки сторони в такому трикутнику є рівними («a = a», «b = a»), то будемо мати множення двох однакових сторін, тобто «a²», та всі кути такого трикутника є по «60» градусів («y = 60»), а «sin ⁡60 = #3#2». То підставивши ці значення у формулу «2» будемо мати:

S = /1/2 ab sin ⁡y = /1/2 a∙a sin⁡ 60 = /1/2 a²∙/3/2 = a² 34

Якщо ви пригадаєте теорему синусів та виведе з неї сторони через кути, то зможете підставити отриманий результат в другу формулу. Після чого зможете отримати додаткові формули площі.

Пригадаємо формулу синусів:

/a/sin⁡ α = /b/sin ⁡β = /c/sin ⁡γ = 2R

Де «a», «b», «c» сторони трикутника; «α», «β», «γ» протилежні кути до сторін; «R» радіус описаного кола.

Для прикладу, якщо ми візьмемо дві перші частини («/a/sin⁡ α = /b/sin ⁡β») і виразимо з них змінну «b», то отримаємо:

b = /a · sin⁡ β/sin ⁡α

Тепер, якщо ми підставимо це у другу формулу («S = /1/2 · ab · sin⁡ y»), то отримаємо:

S = /1/2 a ∙ /a sin ⁡β/sin ⁡α ∙ sin ⁡y

Або це ще можна записати так:

S = a² · sin ⁡β · sin ⁡γ2 · sin ⁡α

Також, ми можемо взагалі позбутися від значення сторін. Для цього необхідно взяти першу та четверту частину теореми синусів («/a/sin ⁡α = 2R»). Та виразити з неї змінну «a»:

a = 2R sin⁡ α

І замість «a» підставити отриманий результат у попередню формулу:

S = (2R · sin ⁡α)² · sin ⁡β · sin ⁡γ2 · sin ⁡α

Виконавши всі спрощення ми отримаємо таку формулу для пошуку площі за радіусом описаного кола та кутами трикутника:

S = 2R² · sin⁡ α · sin⁡ β · sin ⁡γ

Площі чотирикутників

Для чотирикутників є також дві формули які можна майже завжди застосовувати.

1. Якщо відомі дві сторони чотирикутника («a», «b») та відомий кут між цими сторонами («y»), то можна скористатися такою формулою:

S = ab·sin ⁡y

2. Якщо відомі обидві діагоналі чотирикутника («d₁», «d₂») та кут між цими діагоналями («y»), то можна скористатися такою формулою:

S = /1/2 d₁d₂ sin ⁡y

Це все через те, що майже всі базові чотирикутники є різновидами паралелограма. А, дані формули як раз є формулами площі паралелограма.

Квадрат

1. Якщо нам відома сторона квадрата («a»), то площу можна знайти за формулою:

S = a²

Це є перша формула із загальних. Оскільки сторони квадрата рівні, то будемо мати «a ∙ a = a²» і кути між сторонами є «90» градусів, а «sin ⁡90 = 1». Зважаючи на це отримаємо нашу формулу.

2. Якщо відома діагональ квадрата («d»), то площу можна знайти за такою формулою:

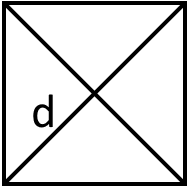
S = /1/2 d²

Це є друга формула із загальних. Оскільки діагоналі квадрата є рівні та перетинаються під прямим кутом (тобто кут між діагоналями буде «90» градусів), то відповідно і отримаємо «d ∙ d = d²», «sin⁡ 90 = 1».

Прямокутник

1. Якщо відомі дві не протилежні сторони прямокутника («a», «b»), то:

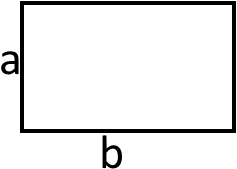
S = ab

Це є перша формула із загальних. Синус зникає через те, що кути між сторонами прямокутника рівні «90» градусів.

2. Якщо будемо мати діагональ прямокутника («d») та кут між діагоналями («y»), то:

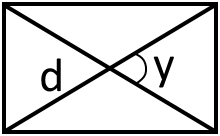
S = /1/2 d² sin ⁡y

Це буде друга формула із загальних. Оскільки діагоналі в прямокутнику рівні тому будемо мати «d ∙ d = d²».

Паралелограм

1. Якщо у паралелограмі відома сторона («a» або «b») та висота проведена до цієї сторони («h_a» або «h_b»), то:

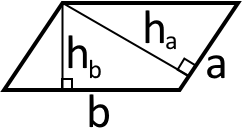
S = ah_a = bh_b

2. Якщо будуть відомі дві сторони паралелограма («a», «b») та кут між цими сторонами («у»), то:

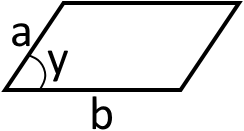
S = ab · sin ⁡y

Як бачите це є абсолютно така ж формула як перша із загальних.

3. Якщо будуть відомі діагоналі («d₁», «d₂») та кут між діагоналями («y») паралелограма, то:

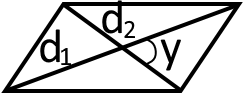
S = /1/2 d₁d₂ sin ⁡y

Як бачите це є абсолютно така ж формула як друга із загальних.

Ромб

1. Якщо буде відомо сторону («a») та висоту («h») ромба, то:

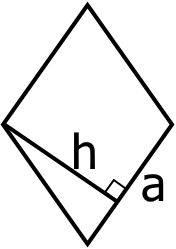
S = ah

2. Якщо буде відомо сторону («a») та будь-який кут («у») ромба, то:

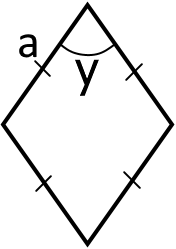
S = a² sin ⁡y

Це є перша із загальних формул. Оскільки у ромба всі сторони рівні, то маємо «a ∙ a = a²».

3. Якщо відомі діагоналі («d₁», «d₂») ромба, то:

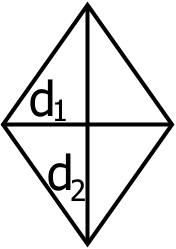
S = /1/2 d₁d₂

Це є друга формула із загальних. Оскільки діагоналі в ромбі перетинаються під прямим кутом, то буде «sin ⁡90⁰ = 1». Через, що він зникає.

Трапеція

1. Якщо буде відомо обидві основи («a», «b») та висоту («h») трапеції, то:

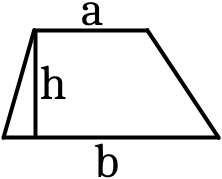
S = /a + b/2h

2. Якщо будуть відомі діагоналі («d₁», «d₂») трапеції та кут між ними («y»), то:

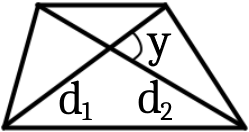
S = /1/2 d₁d₂ sin ⁡y

Як бачите це друга формула із загальних.

Правильний багатокутник

Для пошуку площі правильного багатокутника часто використовують описане коло. Також кожен правильний багатокутник можна розбити на рівнобедрені трикутники кількість яких буде рівна кількості кутів багатокутника. Радіус описаного кола буде рівний половині діагоналі яка проходить через центр описаного кола.

Отже будемо мати такі формули для знаходження площі правильного многокутника:

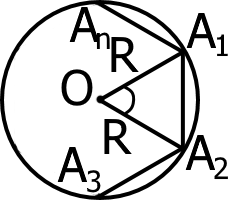
S = n ∙ S_{∆ A1OA2}

S = /n/2 R² sin⁡ ∠ A₁OA₂

S = /n/2 R² sin⁡/360/n

В реальності формули «S = /n/2 R² sin⁡ ∠ A₁OA₂» та «S = /n/2 R² sin⁡/360/n» це є та ж сама формула «S = n ∙ S_{∆ A1OA2}». Просто, в даних формулах вже є розписана площа трикутника. Нам відома така формула площі трикутника: «S = /1/2 ab sin ⁡y». Де «a» та «b» це сторони трикутника, а «y» кут між цими сторонами. В якості сторін трикутника обираємо «OA₁» та «OA₂», відповідно кут між ними буде «A₁OA₂». І враховуючи, що «OA₁ = OA₂ = R», то формула площі набуває такого вигляду: «S = /1/2 R · R sin⁡ ∠ A₁OA₂», тобто «S = /1/2 R² sin⁡ ∠ A₁OA₂». Після чого, нам залишається, помножити площу одного трикутника на кількість таких трикутників (тобто, на «n») і ми отримаємо площу правильного «n-кутника». Тобто: «S = n · /1/2 R² sin⁡ ∠ A₁OA₂»

А, врахувавши, що центральний кут правильного «n-кутника» можна знайти як «/360/n», то отримаємо, що «A₁OA₂ = /360/n». Звідси отримаємо дану формулу «S = /n/2 R² sin⁡/360/n».

Довільний багатокутник

Якщо є довільний багатокутник і відомі всі його сторони («a₁», «a₂», …, «a_n») або периметр багатокутника («P») та радіус вписаного кола («r»), то:

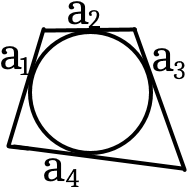
S = /Pr/2 = a₁ + a₂ + ... + a_n2 r

Круг

Якщо є відомий радіус («r»)

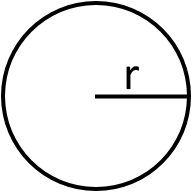
або діаметр («d») круга,

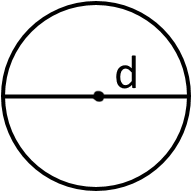
то:

S = πr² = πd²4

Круговий сектор

Якщо відомо радіус («r») круга та градусну міру центрального кута або дуги («n»), то:

S = πr²n360

Якщо відомо радіус («r») круга та радіальну міру центрального кута («α»), то:

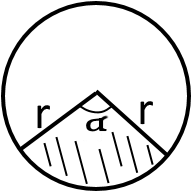
S = r²α2

Круговий сегмент

Круговий сегмент можна знайти знаючи площу кругового сектора та площу трикутника утвореного радіусами круга. Де «r» - радіус круга, «n» - градусна міра центрального кута кругового сектора.

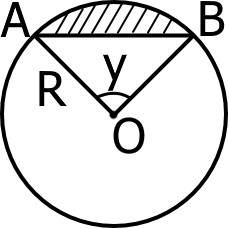
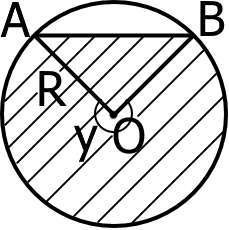
S = πr²n360 ± S_∆AOB

При «n < 180» знак «-», при «n > 180» знак «+».

Кільце

Якщо розглянути, то можна помітити, що це круг з якого вирізали круг меншого радіуса (діаметра). Тобто, ми можемо знайти площу кільця знайшовши площу круга більшого радіуса та відняти площу круга меншого радіуса.

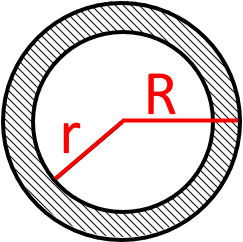
Припустимо, що «R» радіус більшого круга, а «r» - меншого круга. Тоді будемо мати:

S = πR² - πr²

Або

S = π(R² - r²)

Складні фігури

Площу будь-якої складної фігури можна знайти за допомогою суми простих фігур з якої вона складається:

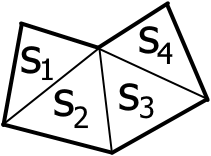
S = S₁ + S₂ + ... + S_n